Norbert Lieven 🏠

Bei Additionen darfst du die Reihenfolge der Summanden vertauschen. Aber wie sieht das bei Subtraktionen aus? Darf man die beiden Minuszahlen vertauschen? Um diese Frage zu beantworten, machst du bitte einen kleinen Versuch. Nimm 3 Farbstifte. Dann rechne mit diesen Stiften die Subtraktion 3 Stifte minus 2 Stifte. Nimm also von diesen 3 Stiften 2 Stifte weg. Als Ergebnis bleibt ein Stift liegen. Die Subtraktion 3-2 ist gleich 1.
Jetzt vertauschst du die beiden Minuszahlen. Lege vor dir 2 Farbstifte und dann nimm hiervon 3 Stifte weg. Hoppala! Wie soll das denn gehen, fragst du dich?
Deine Frage ist berechtigt, denn es geht nicht. Man kann von einer Zahl keine größere Zahl abziehen. Deshalb gibt es einen neuen Merksatz:

Wir schauen uns folgende Aufgabe an: 18-3-2-8=. Du könntest jetzt ganz normal rechnen:
18-3=15, 15-2=13, 13-8=5. Diese Rechenfolge ist aber umständlich, weil man viel rechnen muss.

Durch geschicktes Vertauschen und Bündeln von Zahlen kannst du viel leichter zum Ergebnis kommen.
Hier noch einmal die Aufgabe: 18-3-2-8=. Mit schnellem Blick siehst du, dass du zuerst 18-8 rechnest und 10 erhältst. Mit einem weiteren schnellen Blick bündelst du die Zahlen 3 und 2 zur 5 und ziehst diese 5 von der 10 ab. So erhältst du als Ergebnis die 5. 

Im folgenden Beispiel erkennst du schnell, dass die 7 die Halbierungszahl von der 14 ist, und rechnest deshalb: 14-7-1.

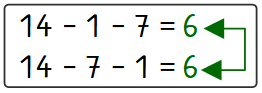
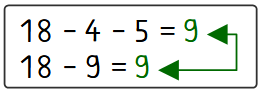
In dieser Aufgabe hilft dir die Halbierungszahl 9 weiter. Erkennst du, woher die 9 kommt?